TOPICS from KATEKYO
【中学生】「数と数字」③(2020.5.16)
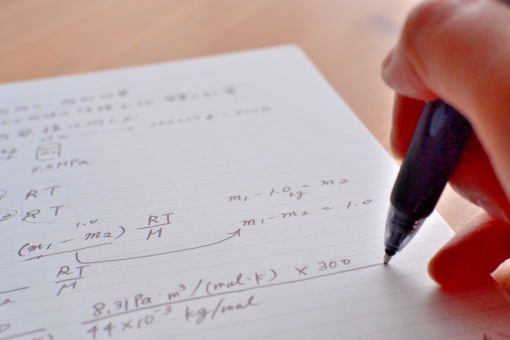
【整数に関する方程式】の代表的な文章題への誤答についてのお話の続きです。
Q:2桁の自然数がある。十の位の数と一の位の数の和は11で、十の位の数と一の位の数を入れ替えた数は、もとの数より27小さいという。もとの自然数を求めなさい。
(再稿となりますが…。)解法のポイントは、求める数の十の位の数をⅹ、一の位の数をyとして、もとの数を10x+y、入れ替えた数を10y+xと表し、連立方程式を立てます。方程式①は、十の位の数と一の位の数の和が11について立式していくのですが…この思考がなかなか難解なのです。ここでもう一度確認したいのが、数【概念】を一度数字【記号】に戻し、再び数【概念】に再構成するということです。(答えは、x+y=11…①となります。)
では、なぜここで多くのつまずきが見られるのでしょうか?
ズバリこれは…数を『位取りの原理と記数法』を基に考えられないことが、大きな原因の1つに挙げられます。この考えは、遡ること小学2年生からの積み上げであり、つながること高校数学(ⅠA整数の性質【n進法】等)まで関わってくる系統なのです。
では、この問題を解消するためには、どうしていけばよいのでしょうか? もう少し、みなさんと考えていきたいと思います。次回をお楽しみに…。
プロ教師:山本一人
各校の「TOPICS」はこちら




